算法和数据结构复习

发表于 2021-05-12 更新于 2021-07-02 阅读次数：

养成自顶向下的编程习惯，参考,类似写报纸新闻一样，主要逻辑放在最上面（新闻标题 ——> 主函数），后面再写具体的细节（正文 ——> 具体的功能子函数）

时间复杂度和空间复杂度：这部分看到具体的代码能够说出来即可（找主要语句的执行次数）

面试时要和面试官把题目的意思和边界条件明确（不要害怕沟通），尽可能想出自己能力范围内的所有解法，然后比较他们之间的时间和空间复杂度，最后写出的最优的解决方案。

主定理（Master Theorem）：用来解决所有递归问题（递归函数）的时间复杂度
主要记住四种常用的即可—-二分查找[一维]、二叉树遍历、排好序的矩阵中进行二分查找[二维]、归并排序
（公式可以看相关课件）

通过主定理可知：
二叉树的前序、中序、后序遍历，图的遍历以及搜索算法（DFS、BFS）的时间复杂度均为 $O(n)$
二分查找：时间复杂度是多少？ $O(log(n))$

数组、链表、跳表

数组查询时间复杂度 $O(1)$ 插入和删除操作 $O(n)$
链表查询时间复杂度 $O(n)$ 插入和删除操作 $O(1)$
为了降低链表的查询时间复杂度 ——-> 跳表（跳表只需理解原理，面试不太会出题考）
跳表的核心思想：升维（空间换时间）
跳表的维护成本很高，插入和删除元素都需要重新更新索引，所以时间复杂度为 $O(logn)$
跳表的空间复杂度为 $O(n)$

解题秘籍：

1.找最近重复子问题

栈、队列、双端队列、优先队列

栈（stack）: 先入后出，添加、删除皆为 $O(1)$，查询为 $O(n)$
队列（queue）: 先入先出，添加、删除皆为 $O(1)$，查询为 $O(n)$
双端队列（Deque: Double-End Queue）: 特殊的队列，头和尾都可以进行出和入；添加、删除皆为 $O(1)$，查询为 $O(n)$
优先队列（Priority Queue）: 插入操作为$O(1)$，取出操作为$O(logN)$ - 按照元素的优先级取出

具有最近相关性的问题 —-> 栈（类比为剥洋葱）

哈希表、映射、集合

哈希表：要存储的对象（例如：字符串）通过哈希函数得到一个下标，该对象按照下标进行存储，所以查询、插入（添加）和删除操作为 $O(1)$

对于 python 语言，hash table 抽象出来即为 dict(或者 json)和 set

树、二叉树、二叉搜索树

二叉树：每个结点都只有左右两个子结点
树和图的区别在于：树是无环的，而图是有环的

Linked List 是特殊化的 Tree
Tree 是特殊化的 Graph

二叉树遍历 Pre-order/In-order/Post-order（很重要）
1.前序（Pre-order）：根-左-右
2.中序（In-order）：左-根-右
3.后序（Post-order）：左-右-根

二叉搜索树 Binary Search Tree
二叉搜索树是指一棵空树或者具有下列性质的二叉树：

左子树上所有结点的值均小于它的根结点的值；
右子树上所有结点的值均大于它的根结点的值；
以此类推：左、右子树也分别为二叉查找树。（这就是重复性！）
其查询，插入和删除操作的时间复杂度均为 $O(log(n))$

二叉搜索树的中序遍历：升序排列

泛型递归、树的递归

树的面试题解法一般都是递归(树结构本身的定义以及其重复性)

递归 - 循环
通过函数体来进行的循环

Python 代码模版

def recursion(level, param1, param2, ...):
    # recursion terminator
    if level > MAX_LEVEL:
    process_result
    return
    # process logic in current level
    process(level, data...)
    # drill down
    self.recursion(level + 1, p1, ...)
    # reverse the current level status if needed

分治、回溯（Divide & Conquer、Backtracking）

可以认为分治和回溯是一种特殊的递归
最近重复性 —-> 分治，回溯
最优重复性 —-> 动态规划

深度优先搜索和广度优先搜索

搜索-遍历

每个节点都要访问一次
每个节点仅仅要访问一次
对于节点的访问顺序不限
深度优先：depth first search —-> 栈
广度优先：breadth first search —-> 队列

DFS

示例代码-二叉树遍历

def dfs(node):
    if node in visited:
        # already visited
        return
    visited.add(node)
    # process current node
    # ... # logic here
    dfs(node.left)
    dfs(node.right)

示例代码-多叉树遍历（递归写法）

visited = set()
def dfs(node, visited):
    if node in visited: # terminator
        # already visited
        return
    visited.add(node)
    # process current node here.
    ...
    for next_node in node.children():
        if not next_node in visited:
            dfs(next_node, visited)

示例代码-树的遍历（非递归写法）

def DFS(self, tree):
    if tree.root is None:
        return []
    visited, stack = [], [tree.root]
    while stack:
        node = stack.pop()
        visited.add(node)
        process (node)
        nodes = generate_related_nodes(node)
        stack.push(nodes)
    # other processing work
    ...

BFS

示例代码

def BFS(graph, start, end):
    queue = []
    queue.append([start])
    visited.add(start)
    while queue:
        node = queue.pop()
        visited.add(node)
        process(node)
        nodes = generate_related_nodes(node)
        queue.push(nodes)
    # other processing work
    ...

贪心算法

贪心算法是一种在每一步选择中都采取在当前状态下最好或最优（即最有利）的选择，从而希望导致结果是全局最好或最优的算法。

贪心算法与动态规划的不同在于它对每个子问题的解决方案都做出选择，不能回退。动态规划则会保存以前的运算结果，并根据以前的结果对当前进行选择，有回退功能。

贪心：当下做局部最优判断
回溯：能够回退
动态规划：最优判断 + 回退

适用贪心算法的场景
简单地说，问题能够分解成子问题来解决，子问题的最优解能递推到最终问题的最优解。这种子问题最优解称为最优子结构。

二分查找

二分查找的前提

目标函数单调性（单调递增或者递减）
存在上下界（bounded）
能够通过索引访问（index accessible)

代码模版

left, right = 0, len(array) - 1
while left <= right:
    mid = (left + right) / 2
    if array[mid] == target:
        # find the target!!
        break or return result
    elif array[mid] < target:
        left = mid + 1
    else:
        right = mid - 1

动态规划

分治, 回溯, 递归, 动态规划的本质：寻找重复性

找到最近最简方法，将其拆解成可重复解决的问题

关键点

动态规划和递归或者分治没有根本上的区别（关键看有无最优的子结构）
共性：找到重复子问题
差异性：最优子结构、中途可以淘汰次优解

高级动态规划

分治 + 最优子结构 + 记忆化缓存 —-> 动态规划

通常用 顺推形式(动态递推) 代替递归来解决问题

DP 顺推模板:

def function DP():
    dp = [][] # ⼆维情况
    for i = 0 .. M {
        for j = 0 .. N {
            dp[i][j] = _Function(dp[i’][j’]…)
        }
    }
return dp[M][N];

字典树和并查集

字典树(trie)

基本结构：
字典树，即 Trie 树，又称单词查找树或键树，是一种树形结构。典型应用是用于统计和排序大量的字符串（但不仅限于字符串），所以经常被搜索引擎系统用于文本词频统计。

它的优点是：最大限度地减少无谓的字符串比较，查询效率比哈希表高。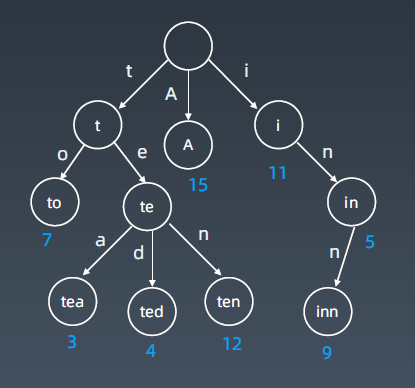
Trie树.PNG

基本性质

结点本身不存完整单词；
从根结点到某一结点，路径上经过的字符连接起来，为该结点对应的字符串；
每个结点的所有子结点路径代表的字符都不相同。

核心思想
Trie 树的核心思想是空间换时间。
利用字符串的公共前缀来降低查询时间的开销以达到提高效率的目的。

并查集(Disjoint Set)

适用场景： 组团，配对

基本操作：

makeSet(s)：建立一个新的并查集，其中包含 s 个单元素集合。
unionSet(x, y)：把元素 x 和元素 y 所在的集合合并，要求 x 和 y 所在的集合不相交，如果相交则不合并。
find(x)：找到元素 x 所在的集合的代表，该操作也可以用于判断两个元素是否位于同一个集合，只要将它们各自的代表比较一下就可以了。

高级搜索

对初级搜索进行优化：不重复（fibonacci）、剪枝（生成括号问题）

不重复是指去除递归中的重复计算，剪枝是指及时减去次优的分支
对搜索方向进行优化：双向搜索（前后BFS）、启发式搜索/A*算法（利用优先队列）

A*搜索基于BFS，只不过在队列 popleft() 的时候是按照自定义的优先级进行弹出

高级树、AVL 树和红黑树

为了保证二叉搜索树的二维维度，防止极端情况出现导致树退化为链表，引入平衡二叉树

AVL 树

Balance Factor（平衡因子）：是它的左子树的高度减去它的右子树的高度（有时相反）。balance factor = {-1, 0, 1} —-> 查询复杂度是树的深度，为了保证左右的深度不要差太多，引入平衡因子
通过旋转操作来进行平衡（四种）: 左旋、右旋、左右旋、右左旋

下图为平衡的 AVL树，即所有节点的平衡因子均在 -1 和 1 之间：

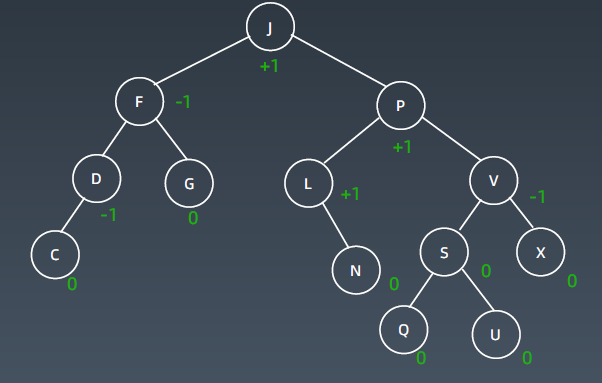
AVL平衡树.PNG

AVL 总结:

平衡二叉搜索树(自平衡)
每个结点存 balance factor = {-1, 0, 1}
四种旋转操作

不足: 结点需要存储额外信息、且调整次数频繁
为了减少 AVL树调整的次数，现实情况是不需要像 AVL树那样严格的平衡 ——> 近似平衡二叉树

红黑树

红黑树是一种近似平衡的二叉搜索树（Binary Search Tree），它能够确保任何一个结点的左右子树的高度差小于两倍。具体来说，红黑树是满足如下条件的二叉搜索树：

每个结点要么是红色，要么是黑色
根节点是黑色
每个叶节点（NIL节点，空节点）是黑色的。
不能有相邻接的两个红色节点
从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点。

关键性质：
从根到叶子的最长的可能路径不多于最短的可能路径的两倍长。

具体红黑树如下图所示：

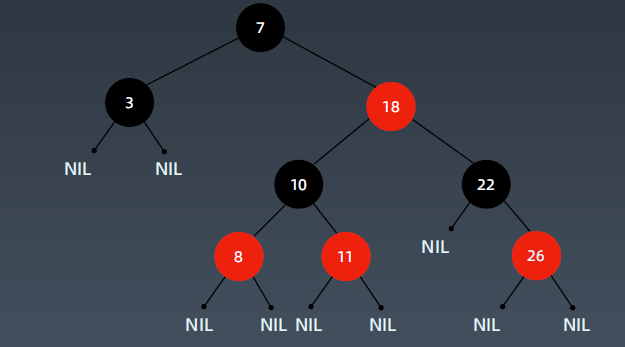
红黑.PNG

AVL树和红黑树的对比

AVL trees provide faster lookups than Red Black Trees because they are more strictly balanced.
Red Black Trees provide faster insertion and removal operations than AVL trees as fewer rotations are done due to relatively relaxed balancing.
AVL trees store balance factors or heights with each node, thus requires storage for an integer per node whereas Red Black Tree requires only 1 bit of information per node.
Red Black Trees are used in most of the language libraries like map, multimap, multisetin C++ whereas AVL trees are used in databases where faster retrievals are required.

位运算

异或： 相同为 0，不同为 1。异或操作的一些特点：

x ^ 0 = x
x ^ 1s = ~x // 注意 1s = ~0
x ^ (~x) = 1s
x ^ x = 0
c = a ^ b => a ^ c = b, b ^ c = a // 交换两个数
a ^ b ^ c = a ^ (b ^ c) = (a ^ b) ^ c // associative

实战位运算要点：

判断奇偶：
x % 2 == 1 —> (x & 1) == 1
x % 2 == 0 —> (x & 1) == 0
x >> 1 —> x / 2
即： x = x / 2; —> x = x >> 1;
mid = (left + right) / 2; —> mid = (left + right) >> 1;
X = X & (X-1) 清零最低位的 1
X & -X => 得到最低位的 1
X & ~X => 0

布隆过滤器、LRU Cache

布隆过滤器(Bloom Filter)

布隆过滤器可以和哈希表进行对比记忆，布隆过滤器只需要判断元素是否存在，而哈希表还需要存储要查询的元素值和其他额外信息。

Bloom Filter vs Hash Table:
布隆过滤器由一个很长的二进制向量和一系列随机映射函数组成。布隆过滤器可以用于检索一个元素是否在一个集合中。

优点：空间效率和查询时间都远远超过一般的算法，
缺点：有一定的误识别率和删除困难。

布隆过滤器可以作为数据库查询操作前的缓存，如果元素不在布隆过滤器中，可以肯定该元素不在数据库中；但如果布隆过滤器判断该元素存在，我们无法保证其一定存储在数据库中。

案例：

比特币网络
分布式系统（Map-Reduce） — Hadoop、search engine
Redis 缓存
垃圾邮件、评论等的过滤

LRU Cache

LRU: Least Recently Used的缩写，即最近最少使用

LRU Cache 两个要素：大小(缓存的大小) 、替换策略
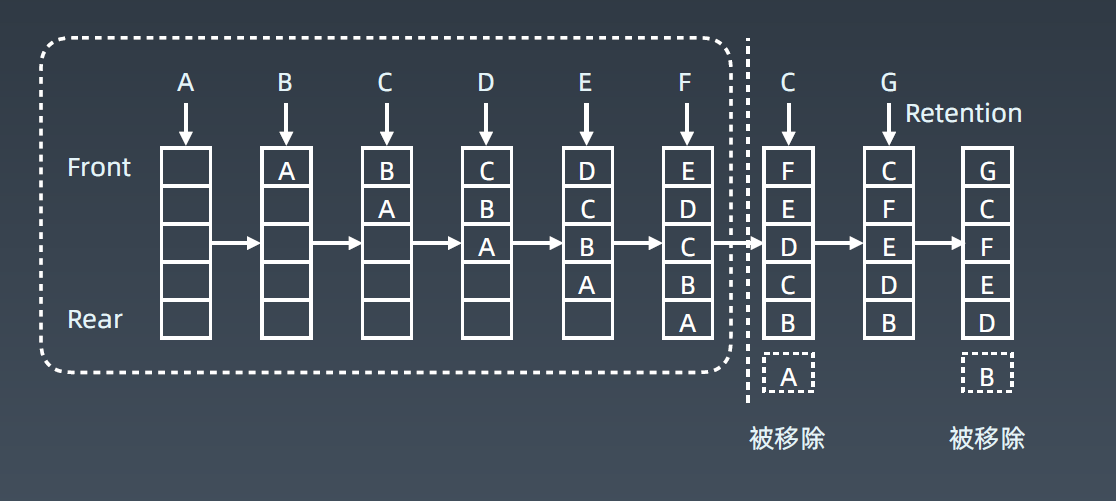
LRU Cache 实现：Hash Table + Double LinkedList —-> O(1) 查询; O(1) 修改、更新

具体工作示例如下图所示：

排序算法

1. 比较类排序：
通过比较来决定元素间的相对次序，由于其时间复杂度不能突破 O(nlogn)，因此也称为非线性时间比较类排序。

2. 非比较类排序(一般只能用于整型相关的数据类型)：
不通过比较来决定元素间的相对次序，它可以突破基于比较排序的时间下界，以线性时间运行，因此也称为线性时间非比较类排序。

排序算法主要理解比较类排序，而比较类排序中时间复杂度为 $O(nlogn)$ 的算法是重点（堆排序，快速排序和归并排序）

初级排序 - O(n^2)

1. 选择排序（Selection Sort）
每次找最小值，然后放到待排序数组的起始位置。

2. 插入排序（Insertion Sort）
从前到后逐步构建有序序列；对于未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入。

3. 冒泡排序（Bubble Sort）
嵌套循环，每次查看相邻的元素如果逆序，则交换。

高级排序 - O(N*LogN)

1. 快速排序（Quick Sort）
数组取标杆 pivot，将小于标杆的元素放 pivot左边，大于标杆的元素放右侧，然后依次对右边和右边的子数组继续快排；以达到整个序列有序。

2. 归并排序（Merge Sort）— 分治

把长度为 n 的输入序列分成两个长度为 n/2 的子序列；
对这两个子序列分别采用归并排序；
将两个排序好的子序列合并成一个最终的排序序列。

归并和快排具有相似性，但步骤顺序相反
归并：先排序左右子数组，然后合并两个有序子数组
快排：先调配出左右子数组，然后对于左右子数组进行排序

3. 堆排序（Heap Sort） — 堆插入 O(logN)，取最大/小值 O(1)

数组元素依次建立小顶堆
依次取堆顶元素，并删除

特殊排序 - O(n)

1. 计数排序（Counting Sort）
计数排序要求输入的数据必须是有确定范围的整数。将输入的数据值转化为键存储在额外开辟的数组空间中；然后依次把计数大于 1 的填充回原数组。

2. 桶排序（Bucket Sort）
桶排序 (Bucket sort)的工作的原理：假设输入数据服从均匀分布，将数据分到有限数量的桶里，每个桶再分别排序（有可能再使用别的排序算法或是以递归方式继续使用桶排序进行排）。

3. 基数排序（Radix Sort）
基数排序是按照低位先排序，然后收集；再按照高位排序，然后再收集；依次类推，直到最高位。有时候有些属性是有优先级顺序的，先按低优先级排序，再按高优先级排序。

字符串

字符串基本操作

遍历，比较，反转，异位词和回文串等。

高级字符串算法

字符串 + 动态规划： 公共子串和公共子序列相关问题以及编辑距离。

字符串匹配算法

字符串匹配：在一个字符串中判断是否包含另一个字符串，并返回其所在位置。

1. 暴力法（brute force） - O(mn)
2. Rabin-Karp 算法
3. KMP 算法
4. Boyer-Moore 算法
5. Sunday 算法

Rabin-Karp 算法： 在暴力法的第二层循环比较时进行优化，使用hash函数先进行片段比较，hash值相同之后再进行逐个比较。

假设子串的长度为 M (pat)，目标字符串的长度为 N (txt)
计算子串的 hash 值 hash_pat
计算目标字符串txt中每个长度为 M 的子串的 hash 值（共需要计算 N-M+1次）
比较 hash 值：如果 hash 值不同，字符串必然不匹配; 如果 hash 值相同，还需要使用朴素算法再次判断

KMP 算法： 利用之前匹配正确的信息（next数组）来加速模式字符串的移动速度。
具体细节参考：如何更好地理解和掌握 KMP 算法?

def buildNxt(p):
    nxt = [0]
    now, x = 0, 1

    while x < len(p):
        if p[now] == p[x]:
            now += 1
            x += 1
            nxt.append(now)
        elif now:
            now = nxt[now-1]
        else:
            nxt.append(0)
            x += 1
    return nxt

def KMP(s, p, nxt):
    tar, pos = 0, 0
    res = []
    while tar < len(s):
        if s[tar] == p[pos]:
            tar += 1
            pos += 1
        elif pos:
            pos = nxt[pos-1]
        else:
            tar += 1

        if pos == len(p):
            res.append(tar-pos)
            pos = nxt[pos-1]
    return res

-------------本文结束感谢您的阅读-------------