文本特征提取（embedding）

发表于 2021-01-28 更新于 2021-04-19 分类于 NLP 阅读次数：

前言

在NLP领域的任务中，为了使模型便于训练，需要将词语或文本表征为固定长度的数值特征向量，最开始使用的便是词袋表征方法（BOW），类似于one-hot编码，区别在于向量中的每个元素是相应单词在文本中出现的统计次数。但是这种方法无法区别下述情况：

This is the first document.
Is this the first document?

虽然两个句子表达的含义不同，但是通过BOW表征的向量确是相同的。为了解决该问题，需要加入位置顺序的信息，除了1-grams，还需要提取2-grams或者更高的grams特征：

Bi-grams are cool!
[‘bi’, ‘grams’, ‘are’, ‘cool’, ‘bi grams’, ‘grams are’, ‘are cool’]

但是在大型的语料库中，有许多词出现的频率非常高（例如：“的”, “是”，“你”，“我”），但是这些词包含的有用信息确很少，如果直接将语料库中统计的单词出现次数作为特征输入到模型中，出现多次但无用的词会在模型中降低出现次数虽少但是包含信息量很大的词的作用，比如某一专业领域的专有名词。为了解决这一问题，需要给不同的词以不同的权重，tf-idf便是一种计算权重的方法。

1. tf-idf

该方法最初用在信息检索（搜索引擎网页排序），后来被NLP领域借鉴用来做文本的embedding。tf-idf两部分的具体含义如下：

tf: term-frequency 词频
idf: inverse document-frequency 逆文本频率

$tf-idf(t,d)=tf(t,d)\times idf(t)$

$tf(t,d)$: 单词 $t$ 在指定文本 $d$ 中出现的次数（$t$在英文资料中其实是term的缩写，因为毕竟n-grams并不都是单词，但中文我也不知道怎样翻译合适:disappointed:)

$idf(t)=log\frac{n}{df(t)}+1$
上式中，$n$表示语料库中文章的总数，$df(t)$表示语料库中包含单词$t$的文章个数。

scikit-learn实现

由于类TfidfVectorizer集合了CountVectorizer和TfidfTransformer两者的功能，所以直接使用TfidfVectorizer获得文本向量，具体如下所示

>>> from sklearn.feature_extraction.text import TfidfVectorizer
>>> vectorizer = TfidfVectorizer()
>>> vectorizer.fit_transform(corpus)
<4x9 sparse matrix of type '<... 'numpy.float64'>'
    with 19 stored elements in Compressed Sparse ... format>

其实scikit-learn官网中给出了具体的例子计算tf-idf，过程很详细，链接见本文的参考[1]。

TfidfVectorizer类中有许多参数，个人觉得比较重要的如下：

stop_words: 可以根据任务不同给定不同的停用词表
ngram_range: 给定n-grams的取值范围
max_df: 构建词表时，如果某个词的文本频率高于max_df就忽略该词
min_df: 构建词表时，如果某个词的文本频率低于max_df就忽略该词
vocabulary: 给定自定义的词表，这样会按照自定义词表的维度计算
smooth_idf: 平滑处理，mooth_idf=True时， $idf(t)=log\frac{1+n}{1+df(t)}+1$
sublinear_tf: sublinear_tf=True时，用$1+log(tf)$替换$tf$

TfidfVectorizer类的定义如下：

class sklearn.feature_extraction.text.TfidfVectorizer(*, input='content', encoding='utf-8', decode_error='strict', strip_accents=None, lowercase=True, preprocessor=None, tokenizer=None, analyzer='word', stop_words=None, token_pattern='(?u)\b\w\w+\b', ngram_range=(1, 1), max_df=1.0, min_df=1, max_features=None, vocabulary=None, binary=False, dtype=<class 'numpy.float64'>, norm='l2', use_idf=True, smooth_idf=True, sublinear_tf=False)

2. word2vec

word2vec在NLP领域应该有着里程碑式的意义，极大推动了NLP领域的研究进展。从大的概念上来讲，word2vec统指用一定维度的稠密向量表示词含义的方法，即将词语嵌入到高维向量空间中。这些嵌入到高维空间的词向量可以识别同义词，反义词或同类别的词，如人、动物、地点、植物、名字或概念等。

相比于之前的词表示方法，word2vec词向量能够捕捉更加丰富的目标词含义（语义），而且word2vec模型包含了词之间的关系信息以及词的相似性，所以word2vec词向量可以很好的解决之前词表示无法解决的简单推理和类比问题，例如：

wv[“king”] + wv[“woman”] - wv[“man”] = wv[“queen”]

神经网络语言模型

要想知道word2vec如何训练词向量，我们要先了解神经网络语言模型，因为神经网络语言模型是word2vec的基础，神经网络的具体结构如下图所示：

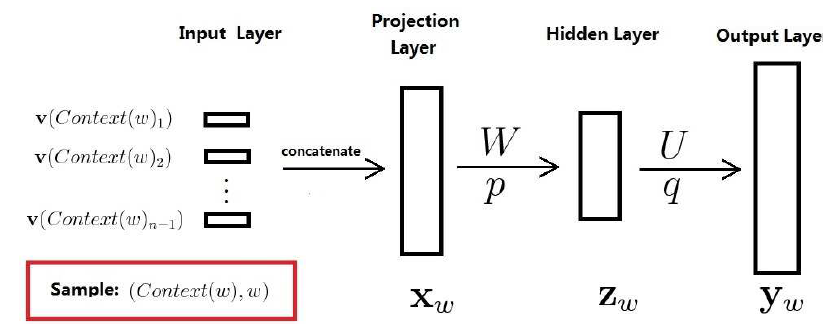
神经网络语言模型.PNG

神经网络语言模型的训练目标是：给定文本中的前几个词（类似n-grams）来预测下一个单词，即 $context(w) ==> p(w|context(w))$ 根据训练目标，我们很容易知道网络的输入和输出是什么，网络的输入是$content(w)$的向量化表示（可以用单词的one-hot编码），$p(w|context(w))$是网络输出经过softmax后的结果。从上面的过程可能看不出这和词向量有什么关系，其实词向量只是网络训练的附属品，当网络训练结束后，从映射层到隐藏层的权重矩阵$W$就是词向量矩阵，词向量矩阵$W$中的每一行即表示词表$V$中某个词的词向量。

word2vec有两个训练词向量的方法：CBOW和skip-gram，在介绍这两种方法之前，需要知道这两种方法所采用的核心思想，即分布式假设：

You shall know a word by the company it keeps - J.R. Firth 1957
如果两个词的上下文是相似的，它们的语义也是相似的。

所以如果两个词经常用于相似的上下文中（与附近相似的词一起使用），则它们的word2vec词向量在词向量空间中也会比较接近。

CBOW(continuous bag-of-words)

核心思想：使用邻近词预测中心词，邻近词根据滑动窗口（window size）进行选择
CBOW网络的输入：滑窗内邻近词one-hot向量（也可以随机初始化）的累加
CBOW训练样本的label：中心词的one-hot编码

基于Hierarchical Softmax的CBOW模型

CBOW模型由三层构成：输入层，投影层和输出层，具体的网络结构如下图所示：

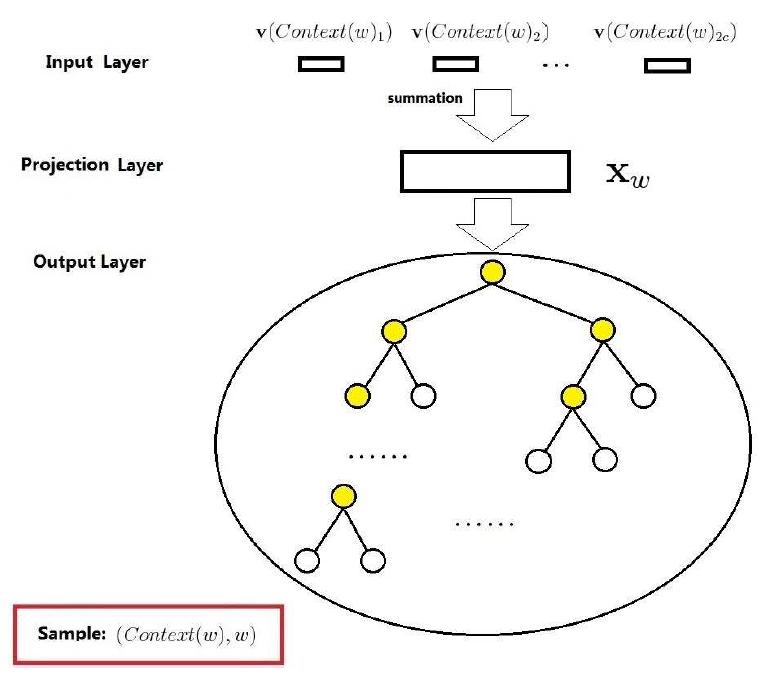
CBOW_分层softmax.PNG
图中 $v(context(w)_1), v(context(w)_1), …, v(context(w)_{2c})$ 表示中心词 $w$ 前 $c$ 和后 $c$ 个邻近词的词向量。投影层做向量的累加操作，即

$sum[v(context(w)_1), v(context(w)_1), ..., v(context(w)_{2c})]$

从CBOW模型网络结构可以看出其与上文介绍的神经网络语言模型有三点不同：

输入层到投影层：CBOW模型用邻近词向量累加代替前者的拼接操作
隐藏层：CBOW模型去除了前者使用的隐藏层
输出层：CBOW模型用huffman树代替前者的softmax操作

基于Hierarchical Softmax的CBOW模型的目标函数定义，训练流程以及梯度计算可以参考[2]，这篇博客由浅入深介绍了word2vec中的数学原理，里面的推导过程非常详细，我之前疑惑的点都是通过这篇博客得以解决。

基于Negative Sampling的CBOW模型

除了Hierarchical Softmax方法，Tomas Mikolov提出的另一个优化技巧是Negative Sampling(负采样)。当一个训练样本输入到网络后，会引起网络中所有权重的更新，这样会改变词汇表中所有词的向量值。但当词汇表的规模达到上亿级别时，显然这种更新所有权重的方法会变得极其低效。所以为了加快词向量模型的训练速度，Tomas Mikolov提出了负采样方法。

负采样核心思想：选取$n$个负样本词对（目标输出词之外的词），根据其对输出的贡献来更新对应的权重。通过这种方法，可以极大地减小计算量，而且对训练网络性能不会有明显影响。

注意：如果是在一个小型语料库上训练词向量，可以使用5~20个样本的负采样率。对于较大型的语料库和词汇表，根据Mikolov团队的建议，可以将负采样率降低到2~5个样本。

基于Negative Sampling的CBOW模型的目标函数定义，训练流程以及梯度计算同样可以参考[2]

skip-gram

核心思想：使用中心词分别预测邻近词，邻近词根据滑动窗口（window size）进行选择
skip-gram网络的输入：中心词的one-hot向量（也可以随机初始化）
skip-gram训练样本的label：每个邻近词的单独one-hot编码

基于Hierarchical Softmax的skip-gram模型

skip-gram模型由三层构成：输入层，投影层和输出层，具体的网络结构如下图所示：

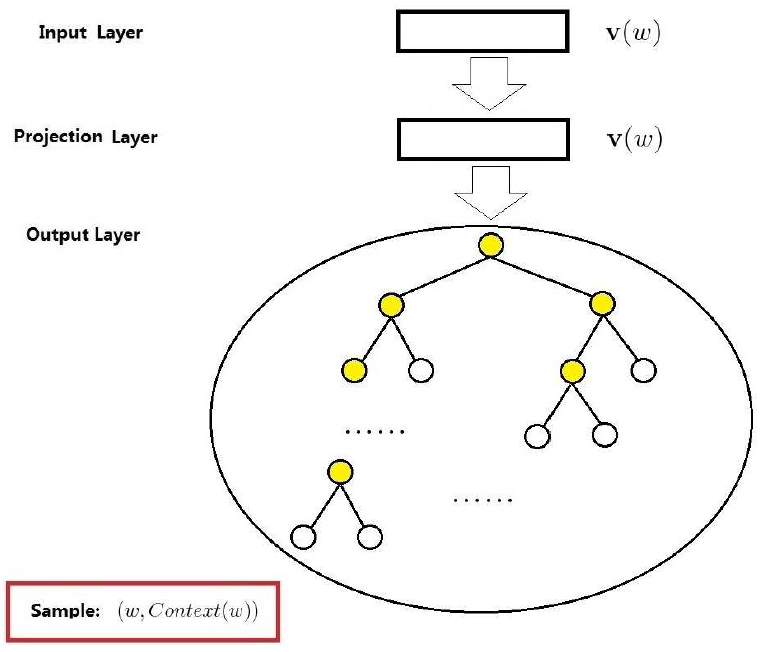
skip_gram分层softmax.PNG
图中 $v(w)$ 表示中心词的词向量，投影层其实可以去除掉。skip-gram模型和CBOW模型的主要区别在于目标函数 $L$ 的定义：

CBOW模型：

$p(w|context(w))=\prod\limits_{j=2}^{l^w}p(d_j^w|X_w,\theta_{j-1}^w)$

$p(d_j^w|X_w,\theta_{j-1}^w)= \begin{cases}
\sigma(X_w^T\theta_{j-1}^w), \qquad\quad\,\,\,\, d_j^w=0\\
1-\sigma(X_w^T\theta_{j-1}^w), \qquad d_j^w=1
\end{cases}
$

$L = \sum\limits_{w\in C}log\,p(w|context(w))=\sum\limits_{w\in C}log\prod\limits_{j=2}^{l^w}\{[\sigma(X_w^T\theta_{j-1}^w)]^{1-d_j^w}\cdot[1-\sigma(X_w^T\theta_{j-1}^w)]^{d_j^w}]\}$

skip-gram模型：

$p(context(w)|w)=\prod\limits_{u\in context(w)}p(u|w)=\prod\limits_{u\in context(w)}\prod\limits_{j=2}^{l^u}p(d_j^u|v(w),\theta_{j-1}^u)$

$L = \sum\limits_{w\in C}log\prod\limits_{u\in context(w)}\prod\limits_{j=2}^{l^u}\{[\sigma(v(w)^T\theta_{j-1}^u)]^{1-d_j^u}\cdot[1-\sigma(v(w)^T\theta_{j-1}^u)]^{d_j^u}]\}$

其中，$l^w$ 表示从huffman树的根节点出发到 $w$ 叶子节点的路径上包含的节点个数，$d_j^w$ 表示该路径上第 $j$ 个非根节点对应的huffman编码，$\theta_j^w$ 表示非叶子节点上对应的参数向量。

基于Negative Sampling的skip-gram模型

在Negative Sampling的方法下，skip-gram模型和CBOW模型的主要区别同样在于目标函数 $L$ 的定义：

CBOW模型：
对于给定的样本 $(context(w), w)$，CBOW模型希望最大化

$g(w)=\prod\limits_{u\in \{w\}\cup NEG(w)}p(u|context(w))$

$p(u|context(w))= \begin{cases}
\sigma(X_w^T\theta^u), \qquad\quad\,\,\,\, L^w(u)=1\\
1-\sigma(X_w^T\theta^u), \qquad L^w(u)=0
\end{cases}$

$L=log\,\prod\limits_{w\in C}g(w)=\sum\limits_{w\in C}log\,g(w)
\\ \,\,\,\,=\sum\limits_{w\in C}log\prod\limits_{u\in \{w\}\cup NEG(w)}
\{[\sigma(X_w^T\theta^u)]^{L^w(u)}\cdot[1-\sigma(X_w^T\theta^u)]^{1-L^w(u)}]\}$

其中$NEG(w)$为关于 $w$ 的负样本子集；当 $u\in \{w\}$ 时，$L^w(u)=1$，否则为 $0$.

skip-gram模型：

$g(w)=\prod\limits_{u\in context(w)}g(u)=\prod\limits_{u\in context(w)}\prod\limits_{z\in \{u\} \cup NEG(u)}p(z|w)$

$p(z|w)= \begin{cases}
\sigma(v(w)^T\theta^z), \qquad\quad\,\,\,\, L^u(z)=1\\
1-\sigma(v(w)^T\theta^z), \qquad L^u(z)=0
\end{cases}$

$L=log\,\prod\limits_{w\in C}g(w)=log\,\prod\limits_{w\in C}\prod\limits_{u\in context(w)}\prod\limits_{z\in \{u\} \cup NEG(u)}p(z|w)
\\ \,\,\,\,=\sum\limits_{w\in C}\sum\limits_{u\in context(w)}log
\prod\limits_{z\in \{u\} \cup NEG(u)}
\{[\sigma(v(w)^T\theta^z)]^{L^u(z)}\cdot[1-\sigma(v(w)^T\theta^z)]^{1-L^u(z)}]\}$

至此，word2vec的训练机理，两种模型（CBOW、skip-gram）及其分别对应的两种方法（分层softmax、负采样）讲述完毕。

训练小技巧

高频 2-gram

训练语料库中，有些词经常和其他词组合出现，例如 “san” 和 “Francisco” 共现频率非常高，但这种预测是没有太大价值的，而且这种组合词通常与其中的单个词表达的意义完全不一样，所以训练时将这种共现词看作一个词 “san_Francisco” (2-gram)，除了 2-gram，也会考虑 3-gram.

训练过程中，如果两个词的得分高于阈值 $\delta$, 则这两个词会当作一个词项放在word2vec的词表中，打分函数如下所示：

$score(w_i, w_j) = \frac{count(w_i, w_j)-\delta}{count(w_i)\times count(w_j)}$

高频词条下采样

像 “the” 或 “a” 这样的常用词通常不包含重要信息，语料库中 “the” 与许多名词都共现，因此并不会带来更多的含义，反而给word2vec语义相似性表示带来一定的混淆。但所有词都是有意义的，比如像 “the” 和 “a” 这样的停用词，又因为词向量会经常用在生成模型中，在这种场景下，词汇表中就必须包含停用词和其他常用词，并且允许这些词影响其相邻词的词向量。

为了减少像停用词这样的高频词的影响，可以在训练过程中对词进行与其出现频率成反比的采样。相比于罕见词，高频词被赋以对向量更小的影响力。对于一个给定词，其采样概率如下所示：

$P(w_i)=1-\sqrt{\frac{t}{f(w_i)}}$

其中，$f(w_i)$ 表示词 $w_i$ 在语料库中出现的频率，$t$ 表示频率阈值，超出这个阈值的单词才会进行下采样。

两种模型的适用场景

Mikolov强调，skip-gram 方法对于小型语料库和一些罕见的词项比较适用。在 skip-gram 方法中，由于网络结构的原因，将会产生更多的训练样本。但 CBOW 方法在常用词上有更高的精确性，并且训练速度会快很多。

3. FastText

前言

word2vec虽然在词表征方面已经达到了很好的效果，但是仍然存在以下两点主要问题：

OOV 问题
word2vec 仅对词表中的每个词训练相应的词向量，对于没有出现在词表中的单词是爱莫能助的，例如：
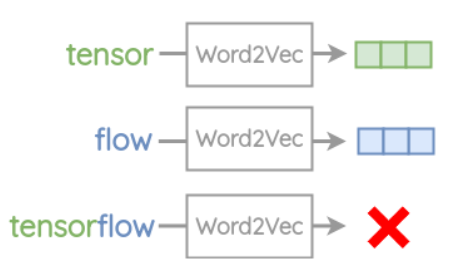
单词形态学的含义
word2vec 基于单词的上下文进行训练，这种方式只考虑了单词的语义信息而没有考虑单词的形态学信息，但是形态学层面的信息也是单词表征的一部分。例如：
$\,$
$embedding[“apparently”] \leftarrow embedding[“apparent”] + embedding[“ly”]$

所以为了解决上述两点问题，Bojanowski et al 提出了新的词嵌入方法，即FastText. FastText在训练过程中额外使用了单词的 n-grams 信息来提高词向量的表征能力。

与 word2vec 的主要区别

word2vec 和 Fasttext 在词向量训练时的主要区别在于网络输入层输入向量的构建方式，下面以 skip-gram 方法为例来说明两者的不同点，参考[3]：

假如训练语料中有一句话为 I am eating food now，用中心词 eating 来预测邻近词 am 和 food

word2vec 直接用 $v(eating)$ 作为输入向量，而 Fasttext 输入向量的构建方式如下图所示：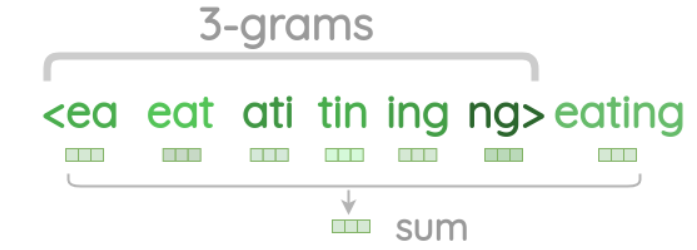

从上图中可以看出 Fasttext 输入向量是中心词和其 n-grams 各元素的向量的累加。

word2vec 和 FastText 的适用场景

gensim 有一个比较 word2vec 和 FastText 不同点的tutorial，可以用作参考。这篇tutorial指出 FastText 的核心是单词的形态结构包含着单词含义的重要信息。

FastText 在 syntactic tasks 上表现要明显好于 word2vec，特别是当训练语料库较小时；但是 word2vec 在 semantic tasks 上要比 FastText 略胜一筹，随着训练语料库的增大这种差异会变小。FastText 的训练时间大概是word2vec的1.5倍。

syntactic tasks 示例：

semantic tasks 示例：

4. GloVe

GloVe 全称为 global vectors of word co-occurrences，从名字中可以看出该方法使用词的共现信息来获得全局的词向量，这也是该方法相较于 word2vec 的优势。从第二小节中我们知道 word2vec 使用的是局部统计信息（滑窗内中心词的上下文信息），但 GloVe 除了使用局部统计信息外还使用了全局统计信息（词共现矩阵）。

个人认为 GloVe方法的重点在于共现矩阵的统计和目标函数的构造，下面给出其具体实现过程：

共现矩阵的统计

共现矩阵是通过滑窗在语料库的移动来依次统计滑窗内中心词和上下文词的共现次数，最后将统计数据放入 $V\times V$（$V$ 是词汇表的大小）大小的对称矩阵中，该矩阵即为共现矩阵。这篇知乎[4]作者给了一个详细的例子可以用作参考。

目标函数的构造

首先定义一些变量：

$X_{ij}$ 表示单词 $j$ 出现在单词的上下文中的次数；
$X_i$ 表示单词 $i$ 的上下文中所有单词出现的总次数，即 $X_i=\sum\limits_k X_{ik}$；
$P_{ij}=P(j|i)=X_{ij}/X_i$，即表示单词 $j$ 出现在单词 $i$ 的上下文中的概率;

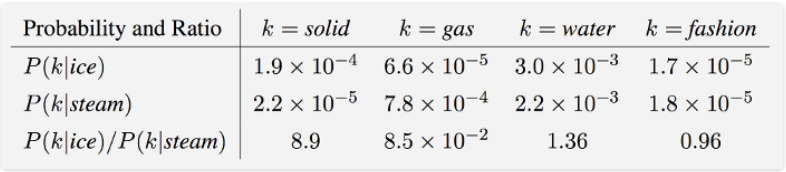
上面表中最后一行的概率比率（Ratio）是重点，glove 的主要工作就是要构造函数来拟合它，如下所示：

$F(w_i,w_j,\widetilde w_k) = \frac{P_{ik}}{P_{jk}}$

接下来转换为用向量差值来表示概率比率（这部分我只能凭直觉理解，参考[5]中的图示也想不出具体理论依据）

$F(w_i-w_j,\widetilde w_k) = \frac{P_{ik}}{P_{jk}}$

经过一系列变换（具体过程参考[6]），论文的作者提出下面的等式来近似表示词向量和共现矩阵的关系：

$w_i^T\widetilde w_j + b_i + \widetilde b_j = log(X_{ij})$

根据该等式便可以构造出如下目标函数：

$J=\sum\limits_{i,j=1}^V f(X_{ij})(w_i^T\widetilde w_j + b_i + \widetilde b_j - log(X_{ij}))^2$

Reference

[1]. scikit-learn中的Text feature extraction部分
 [2]. word2vec中的数学原理详解
 [3]. A Visual Guide to FastText Word Embeddings
[4]. （十五）通俗易懂理解——Glove算法原理
 [5]. Intuitive Guide to Understanding GloVe Embeddings
[6]. GloVe详解

-------------本文结束感谢您的阅读-------------